9.5. Duration modulation (DM) blocks (3dDeconvolve)

Amplitude modulation (AM) can be applied to stimulus timing events in 3dDeconvolve and via afni_proc.py, when stimuli of a given class have varied (but known) durations. One can use the duration modulation (DM) to scale the stimulus responses. This can be applied using -stim_times_AM1 .. and -stim_times_AM2 .. options, and then also specifying a duration block model function, dmBLOCK(...) or dmUBLOCK(...).

There are often questions about which DM block model to pick, and then what parameters to specify for it. Here we briefly describe what the differences are, and provide guidance on making these choices. Essentially, one will choose based on answering 2 questions:

  1. Should the convolved shape height should depend on the stimulus duration?

  2. To what value should the amplitude be scaled?

The choice of answer to Q1 is typically more fundamental, and is almost certainly yes. The answer to Q2 depends slightly on Q1 as well: if the response heights vary, the user essentially picks a representative duration to set the scale.

9.5.1. TL;DR description of block choices

To specify the DM block model, you must specify two features:

  • the function to be used, which could be dmBLOCK or dmUBLOCK,

  • the parenthetical argument to supply, which could be either nothing or a set of parentheses with a number inside.

Given that dmBLOCK, dmUBLOCK and dmUBLOCK(d) (with d<0) are generally considered to be acceptable, what are the differences between them?

  • the shapes of these functions are identical

  • only the scaling differs, and that scaling is constant (and therefore would not affect a t-test statistic, for example)

It is typically recommended to use the dmUBLOCK(...) function with a negative argument value, whose magnitude is the mean response time of the subject or group. Briefly:

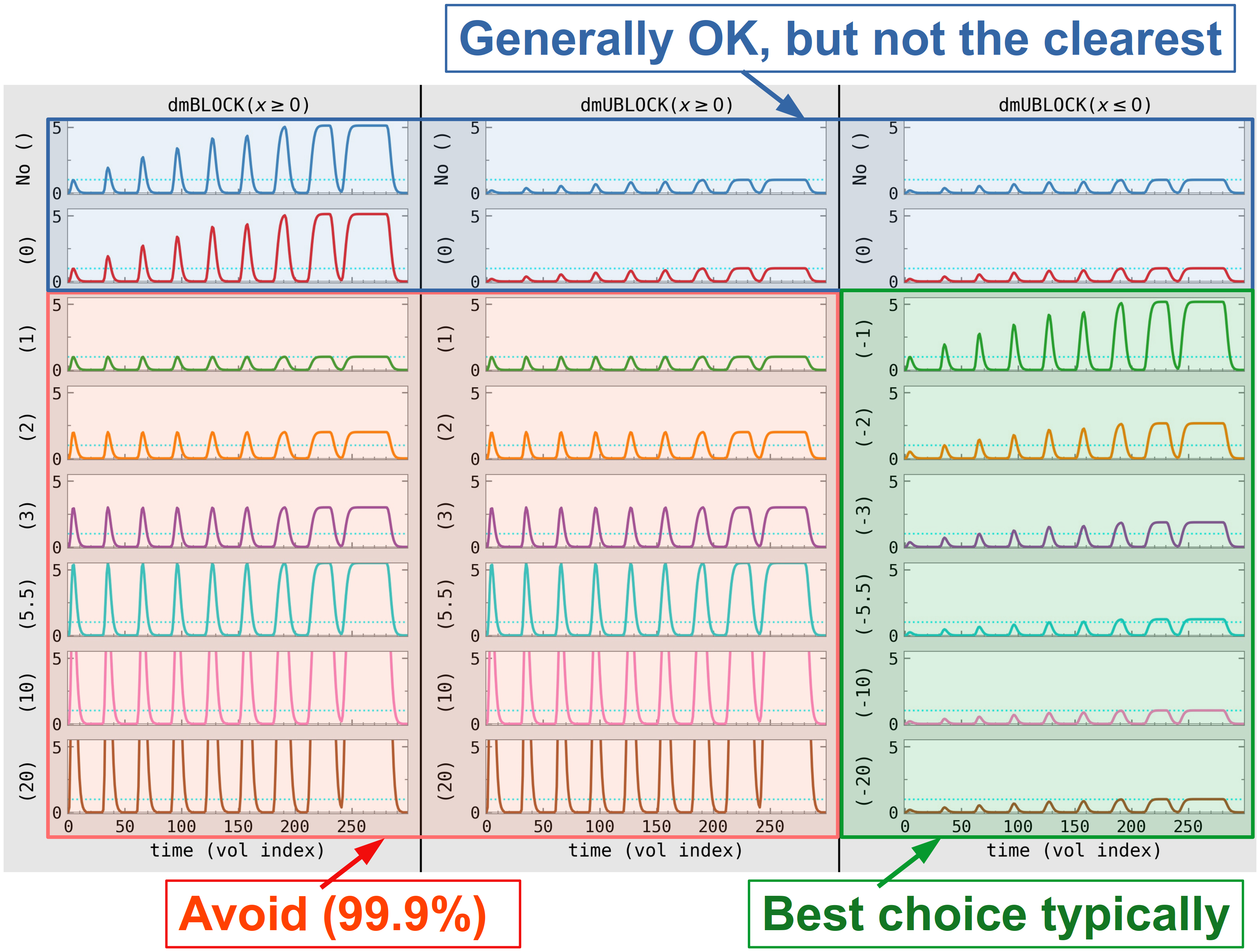
  • In most cases, one uses duration modulation because one wants to have the convolved response amplitude depend on the stimulus duration. That is, the answer to Q1 above is generally “Yes”.
    Therefore, one would avoid cases where the response amplitude would be constant and independent of stimulus duration (below figure, red section; anywhere the argument would be positive).

  • It is often convenient to explicitly pick the stimulus duration whose response gets scaled to unity—that just makes an explanation clearer. Using dmUBLOCK with a negative argument provides that functionality: the magnitude of the argument is the duration whose response gets scaled to unity (below figure, green section; one can’t provide the time-to-scale-to in the blue sections, since no argument is given ).

  • The magnitude of the parameter value is the time whose response will have height of unity. A good way to choose that value would be by calculating the typical time (mean, median or a rounded version of either) of the response durations in a study— providing an answer to Q2 above.
    Generally, the typical response for a subject and for the group should be similar, so you could pick either. If those are not the same... then one must choose what would be most meaningful for the study paradigm and hypothesis.

For example, if the average response time for a subject were 2.4893 s, one might choose dmUBLOCK(-2.5) as the duration modulator.

Figure. A set of example images of convolved models that have the exact same input (the dashed cyan line shows a unit height level). The input timing specification contains successively increasing durations, for didactic purposes. The input timing is formatted as pairs of onset_time:duration_time values, following successively increasing durations (units in seconds; values can be non-integer):
0:1 30:2.5 60:3 90:4 120:5.5 150:6 180:10 210:20 240:40

Examples of dmBLOCK and dmUBLOCK functions (cols) and arguments (rows), commented
../_images/img_all_decon_blocks_X.jpg

9.5.2. Longer description of block choices

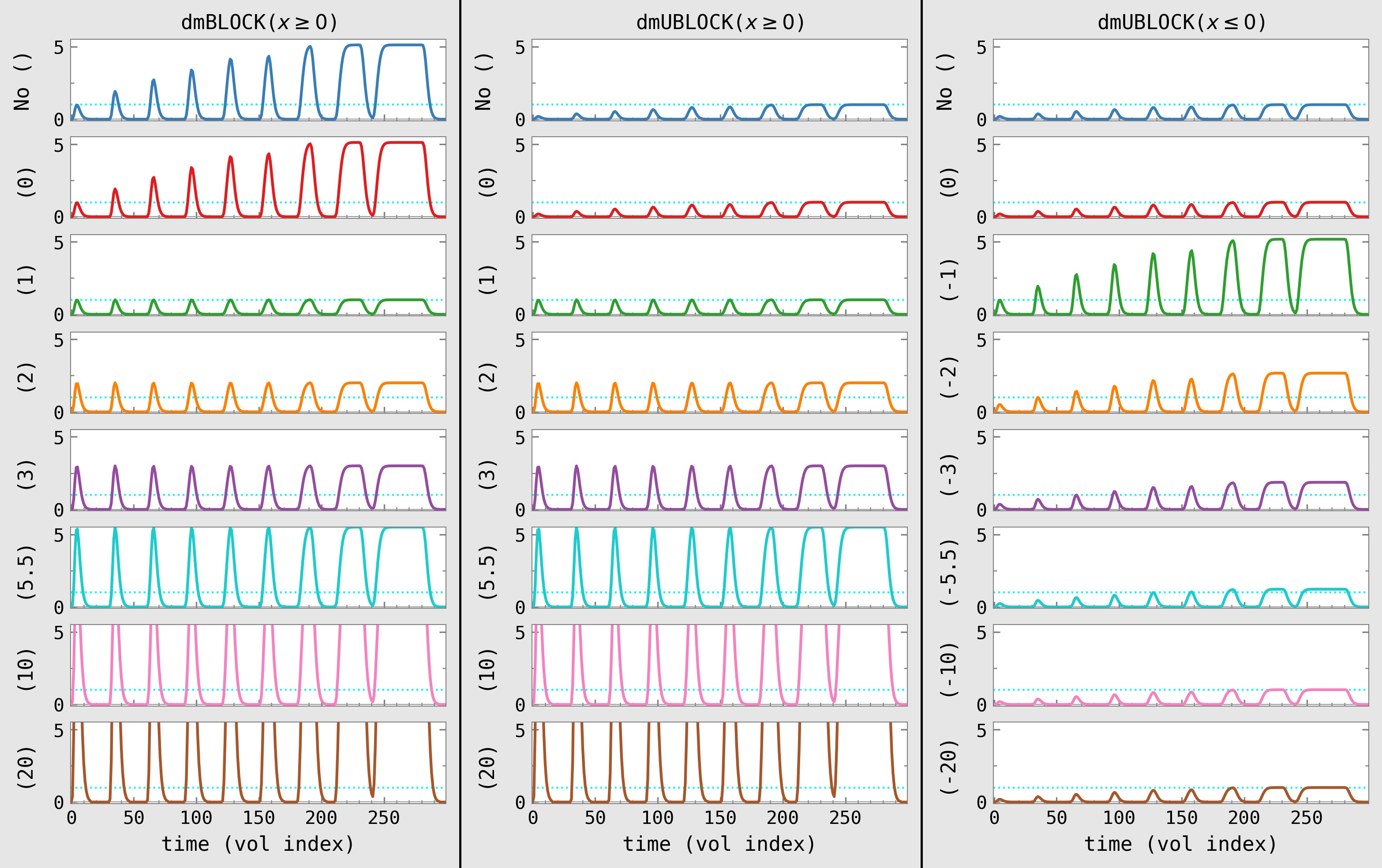
Below are a set of images showing examples of the convolved models for the exact same set of inputs. Each panel shows the resulting convolved response curve, based on the two selections that you, the analyst, make when choosing the DM block:

  • the function to be used, which could be dmBLOCK or dmUBLOCK (see column header),

  • the parenthetical argument to supply, which could be either nothing or a set of parentheses with a number inside (see left of each panel).

In each image, the dashed cyan line shows a unit height level. The input timing specification just shows successively increasing durations, for didactic purposes. It is formatted as pairs of onset_time:duration_time values, following successively increasing durations (units in seconds; values can be non-integer):

0:1 30:2.5 60:3 90:4 120:5.5 150:6 180:10 210:20 240:40

Examples of dmBLOCK and dmUBLOCK functions (cols) and arguments (rows)
../_images/img_all_decon_blocks.jpg

Column 1: The first column shows images with dmBLOCK, which only takes a positive parameter (\geq 0) or no parameter. With no parameter or 0, the convolved response has height 1 for a 1s duration, and the height increases with duration until eventually saturating and plateauing (somewhere between 10 and 20 s). For arguments \geq 1, each convolved response has a constant amplitude, independent of stimulus duration, scaled to the value of the argument itself.

  • So, for this column, if the answer to Q1 above were yes, then the user would use dmBLOCK or dmBLOCK(0) here; and then the answer to Q2 is predetermined, since both of these choices set the scale to be response height of 1 for a 1s stimulus.

  • And if the answer to Q1 were no, then the user would select a any other argument value \geq 1, such as dmBLOCK(1), dmBLOCK(2). Now the answer to Q2 matters, since the argument value picked will be the height of all the responses.

Column 2: The second column shows dmUBLOCK, with either a positive parameter (\geq 0) or no parameter. For arguments \geq 1, this function behaves exactly like dmBLOCK above. When the argument is 0 or no parameter is given, then the response is similar to that of dmBLOCK in that the response amplitude varies, but different to it in that the scaling is such that convolved plateau height is scaled to unity, and short duration events are shorter than 1.

  • So, for this column, if the answer to Q1 above were yes, then the user would use dmUBLOCK or dmUBLOCK(0) here; and then the answer to Q2 is predetermined, since both of these choices set the scale to be response height of 1 for a plateaued stimulus.

  • And if the answer to Q1 were no, then the situation exactly matches that of the dmBLOCK in column 1: the user would select a any other argument value \geq 1, such as dmUBLOCK(1), dmUBLOCK(2). Now the answer to Q2 matters, since the argument value picked will be the height of all the responses.

Note

So, the only difference between dmBLOCK(0) and dmUBLOCK(0) is the scaling, which effectively behaves like a change of units (e.g., using inches vs mm or cm or feet). Within a study, this should have no effect on group level statistics that use subject level effect estimates, because every subject has the same scaling. It might only make a difference when comparing results between studies, or when reporting the values: the user has to specify the scaling used, so a clear comparison can be made.

Column 3: The third column shows dmUBLOCK, with either a non-positive parameter (\leq 0) or no parameter. The first two plots are identical to those of column 2, by definition (response amplitudes vary in height, increasing until a plateau is reached, which is scaled to 1). For negative arguments, the response height now also varies as a function of block duration, with an added bit of clarity: the magnitude of the argument chosen specifies what duration response is scaled to unity. Thus, for dmUBLOCK(-5.5) a 5.5 s stimulus has a response of height 1, a 3 s stimulus has a response height < 1, and a 10 s stimulus has a response height < 1.

  • So, for this column, one must be answering Q1 as yes (because all response heights depend on stimulus duration). Then, one addresses Q2 by choosing what stimulus duration should have a response height of unity; (the negative of) that value is used as the argument.


Taking all of the above into consideration, when choosing a function and parameter in practice, it is typically recommended to use dmUBLOCK(...) with a negative argument value, whose magnitude is the mean response time of the subject or group. Briefly:

  • In most cases, one uses duration modulation because one wants to have the convolved response amplitude depend on the stimulus duration. That is, the answer to Q1 above is generally “Yes”.
    Therefore, one would avoid cases where the response amplitude would be constant and independent of stimulus duration (below figure, red section; anywhere the argument would be positive).

  • It is often convenient to explicitly pick the stimulus duration whose response gets scaled to unity—that just makes explanation clearer. Using dmUBLOCK with a negative argument provides that functionality: the magnitude of the argument is the duration whose response gets scaled to unity (below figure, green section; one can’t provide the time-to-scale-to in the blue sections, since no argument is given ).

  • The magnitude of the parameter value is the time whose response will have height of unity. A good way to choose that value would be by calculating the typical time (mean or median) of the response durations in a study—providing an answer to Q2 above.
    Generally, the typical response for a subject and for the group should be similar, so you could pick either. If those are not the same... then one must choose what would be most meaningful for the study paradigm and hypothesis.

For example, if the average response time for a subject were 2.4893 s, one might choose dmUBLOCK(-2.5) as the duration modulator.


Examples of dmBLOCK and dmUBLOCK functions (cols) and arguments (rows), commented
../_images/img_all_decon_blocks_X.jpg

9.5.3. Additional notes

You can download and peruse additional notes on amplitude modulation here:
AMregression.pdf

9.5.4. Demo image script

In case you are interested, the script used to create these example images is here:
example_3dD_blocks.tcsh.